NUMERICAL ASSESSMENT OF SOME SEMI-ANALYTICAL TECHNIQUES FOR SOLVING A FRACTIONAL-ORDER LEPTOSPIROSIS MODEL
Main Article Content
Abstract
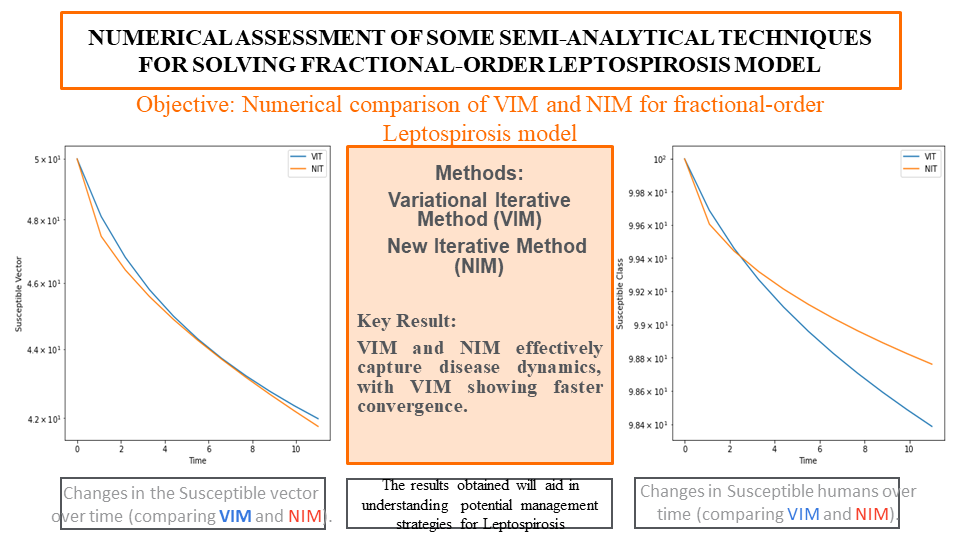
This research aims to apply and compare two semi-analytical techniques, the Variational Iterative Method (VIM) and the New Iterative Method (NIM), for solving a pre-formulated mathematical model of Fractional-order Leptospirosis. Leptospirosis is a significant bacterial infection affecting humans and animals. By implementing the VIM and NIM algorithms, numerical experiments are conducted to solve the leptospirosis model. Comparing the obtained findings demonstrates that VIM and NIM are effective semi-analytical methods for solving systems of fractional differential equations. Notably, our study unveils a crucial dynamic in the disease's spread. The application of VIM and NIM offers a refined depiction of the biological dynamics, highlighting that the susceptible human population gradually decreases, the infectious human population declines, the recovered human population increases, and a significant rise in the infected vector population is observed over time. This nuanced portrayal of the disease's dynamics is crucial for understanding the intricate interplay of Leptospirosis among human and vector populations. The study's outcomes contribute valuable insights into the applicability and performance of the methods in solving the Fractional Leptospirosis model. Results indicate rapid convergence and comparable outcomes for both methods.
Downloads
Article Details
Transfer of Copyrights
- In the event of publication of the manuscript entitled [INSERT MANUSCRIPT TITLE AND REF NO.] in the Malaysian Journal of Science, I hereby transfer copyrights of the manuscript title, abstract and contents to the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) for the full legal term of copyright and any renewals thereof throughout the world in any format, and any media for communication.
Conditions of Publication
- I hereby state that this manuscript to be published is an original work, unpublished in any form prior and I have obtained the necessary permission for the reproduction (or am the owner) of any images, illustrations, tables, charts, figures, maps, photographs and other visual materials of whom the copyrights is owned by a third party.
- This manuscript contains no statements that are contradictory to the relevant local and international laws or that infringes on the rights of others.
- I agree to indemnify the Malaysian Journal of Science and the Faculty of Science, University of Malaya (as the publisher) in the event of any claims that arise in regards to the above conditions and assume full liability on the published manuscript.
Reviewer’s Responsibilities
- Reviewers must treat the manuscripts received for reviewing process as confidential. It must not be shown or discussed with others without the authorization from the editor of MJS.
- Reviewers assigned must not have conflicts of interest with respect to the original work, the authors of the article or the research funding.
- Reviewers should judge or evaluate the manuscripts objective as possible. The feedback from the reviewers should be express clearly with supporting arguments.
- If the assigned reviewer considers themselves not able to complete the review of the manuscript, they must communicate with the editor, so that the manuscript could be sent to another suitable reviewer.
Copyright: Rights of the Author(s)
- Effective 2007, it will become the policy of the Malaysian Journal of Science (published by the Faculty of Science, University of Malaya) to obtain copyrights of all manuscripts published. This is to facilitate:
- Protection against copyright infringement of the manuscript through copyright breaches or piracy.
- Timely handling of reproduction requests from authorized third parties that are addressed directly to the Faculty of Science, University of Malaya.
- As the author, you may publish the fore-mentioned manuscript, whole or any part thereof, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given. You may produce copies of your manuscript, whole or any part thereof, for teaching purposes or to be provided, on individual basis, to fellow researchers.
- You may include the fore-mentioned manuscript, whole or any part thereof, electronically on a secure network at your affiliated institution, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
- You may include the fore-mentioned manuscript, whole or any part thereof, on the World Wide Web, provided acknowledgement regarding copyright notice and reference to first publication in the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers) are given.
- In the event that your manuscript, whole or any part thereof, has been requested to be reproduced, for any purpose or in any form approved by the Malaysian Journal of Science and Faculty of Science, University of Malaya (as the publishers), you will be informed. It is requested that any changes to your contact details (especially e-mail addresses) are made known.
Copyright: Role and responsibility of the Author(s)
- In the event of the manuscript to be published in the Malaysian Journal of Science contains materials copyrighted to others prior, it is the responsibility of current author(s) to obtain written permission from the copyright owner or owners.
- This written permission should be submitted with the proof-copy of the manuscript to be published in the Malaysian Journal of Science
Licensing Policy
Malaysian Journal of Science is an open-access journal that follows the Creative Commons Attribution-Non-commercial 4.0 International License (CC BY-NC 4.0)
CC BY – NC 4.0: Under this licence, the reusers to distribute, remix, alter, and build upon the content in any media or format for non-commercial purposes only, as long as proper acknowledgement is given to the authors of the original work. Please take the time to read the whole licence agreement (https://creativecommons.org/licenses/by-nc/4.0/legalcode ).
References
Ahmad, H. (2018). Variational iteration method with an auxiliary parameter for solving
differential equations of the fifth order, Nonlinear Science Letters A, 9(1), 27–35.
Altaf, K. M., Islam S., & Afzal, K. S. (2014). Mathematical Modeling Towards the Dynamical Interaction of Leptospirosis. Applied Mathematics and Information Sciences, 8, 1049-1056.
Alwehebi, F., Hobiny, A., & Maturi, D. (2023). Variational Iteration Method for Solving Time Fractional Burgers Equation Using Maple. Applied Mathematics, 14, 336-348.
Akogwu, B. O. (2022). Approximate Solutions of Malaria Disease Transmission Model: Using Mult-Step Differential Transform Method, FUDMA Journal of Science, 6(6), 182-194.
Ali, Z., Rabiei F., Rashidi, M. M., & Khodadadi, T. (2022). A fractional-order mathematical model for COVID-19 outbreak with the effect of symptomatic and asymptomatic transmissions. European Physical Journal Plus, 137, 395.
Aslan, I. H., Baca-Carrasco, D., Lenhart, S., & Velasco-Hernandez, J. X. (2021). An age structure model with impulse actions for Leptospirosis in livestock cattle. Journal of Biological Systems, 29(1), 75–105.
Ayoade, A, A., Ibrahim, M. O., & Odetunde, O. (2018). Analytical Solution of a Fractional Order Cholera Model. Nigerian Journal of Scientific Research, 17, 158-164.
Batiha, B., Ghanim, G., & Batiha, K. (2023). Application of the New Iterative Method (NIM) to the Generalized Burgers–Huxley Equation, Symmetry, 15.
Bhalraj,A., & Azmi-Mohd, H. (2021). Analytical and Numerical Solutions of Leptospirosis Model. International Journal of Mathematics and Computer Science, 16(3), 949–961.
Chen, Y., Liu, F. Yu, Q. & Li, T. (2021). Review of fractional epidemic models. Applied Mathematical Modelling, 97, 281–307.
Chong, J. W., Tiong, W. K., Labadin, J. 1., & Sahak, N. (2022). Mathematical modeling of Leptospirosis spread in Malaysia. Mathematical Modeling and Computing, 9(1), 18–25.
Daftardar-Gejji, V., Jafari, H. (2006). An iterative method for solving nonlinear functional equations, Journal of Mathematical Analysis and Applications, 316(2), 753–763.
Darzi, R. & Agheli, B. (2018). An analytic approach for the system of fractional differential equations by means of innovative homotopy perturbation method. Mathematica Moravica, 22(1), 93-105.
Falade, K. I., & Tiamiyu, A. T. (2020a). Computatıonal Algorıthm for the Numerıcal Solutıon of Systems of Volterra Integro-Dıfferentıal Equatıons, Academic Journal of Applied Mathematical Sciences, 6, 66-76.
Falade, K. I., & Tiamiyu, A. T. (2020b) Numerical solution of partial differential equations with fractional variable coefficients using new iterative method (NIM), Mathematical Sciences and Computing, 3, 12-21.
Falade, K. I., Tiamiyu, A. T., & Isa U. (2021). Numerical Comparison of Runge-Kutta (Rk5) and New Iterative Method (Nim) for solving Metastatic Cancer Model. Malaysian Journal of Computing, 6, 758-771.
Falade, K. I., Tiamiyu, A. T., Adio, A. K., Tahir, H. M., Abubakar, U. M., & Badamas, S. M. (2023). Computational Relationship of the Surface Area, and Stiffness of the Spring Constant on Fractional Bagley-Torvik Equation. Turkish Journal of Science & Technology, 18(1), 23-31.
Gomez, A. A., Lopez, M. S., Mullere, G. V., Lopez, L. R., Sione, W., & Giovina, L. (2022). Modeling Leptospirosis outbreaks in relation to hydroclimatic variables in the northeast of Argentina. Heliyon 8(2022).
Gallego, M. A., Simoy, M. V. (2021). Mathematical modeling of leptospirosis: A dynamic regulated by environmental carrying capacity. Chaos, Solitons & Fractals, 152, 114-125.
He, J. H. (2007). Variational iteration method-some recent results and new interpretations. Journal of Computational and Applied Mathematics, 207(1), 3-17.
Khan, M. F., Alrabaiah, H., Altaf, S. M., Farooq, K. M., Mamat, M. & Asjad, M. I. (2021). A new fractional model for vector-host disease with saturated treatment function via singular and non-singular operators. Alexandria Engineering Journal, 60, 629–645.
Khan, M. A., Saeed, I., & Khan, S. A. (2014). Mathematical Modeling towards the dynamical Interaction of Leptospirosis. Applied Mathematics and Information Sciences, 8(3), 1049-1056.
Mousa, M. G., & Altaie, H. O. (2022). Efficient analytical method for the solution of some fractional-order nonlinear differential equations. International Journal of Nonlinear Analytical Application, 13(2), 401–408.
Mukdasai, K., Sabir, Z., Asif, M., Raja, Z., Sadat, R., Ali, M. R., & Singkibud, P. (2022). A numerical simulation of the fractional order Leptospirosis model using the supervised neural Network. Alexandria Engineering Journal, 61, 12431–12441.
Nawaz, R., Ali N., Zada, L., Shah, Z., Tassaddiq, A., & Alreshidi, N. A. (2020). Comparative analysis of natural transform decomposition method and new iterative method for fractional foam drainage problem and fractional order modified regularized long-wave equation,” Fractals, 28(7) article 2050124.
Ngoma, H. D., Kiogora, R. P., & Chepkwony, I. (2022). A Fractional Order Model of Leptospirosis Transmission Dynamics with Environmental Compartment. Global Journal of Pure and Applied Mathematics, 18, 81-110.
Ozlem, D. O. (2020). Modeling the impact of temperature on fractional order dengue model with vertical transmission. International Journal of Optimization and Control: Theories and Applications, 10, 85-93.
Paisanwarakiat, P., & Thamchai, P. (2021). Optimal Control of a Leptospirosis Epidemic Model. Science and Technology Asia, 26(1), 9-17.
Pan, W., Li, T., & Ali, S. (2021). A fractional order epidemic model for the simulation of outbreaks of Ebola. Advances in Difference Equations, 161, 1-21.
Peter, O. J., Oguntolu, F. O., Mayowa, M. O., Oyeniyi, A. O., Jan, R., & Khan, I. (2022). Fractional order mathematical model of monkeypox transmission dynamics. Physica Scripta, 97, 084005.
Ramashis B., & Biswa, F. (2022). Fractional optimal control of compartmental SIR model of COVID-19: Showing the impact of effective vaccination., International Federation of Automatic Control, 55(1), 616–622.
Raouf, R., Zarin, A., & Yusuf, U. W. (2022). Existence theory and numerical solution of leptospirosis disease model via exponential decay law. AIMS Mathematics, 7(5), 8822–8846.
Shihab, M. A., Taha, W. M., Hameed, R. A., Jameel, A., & Ibrahim, S. M. (2023). Implementation of variational iteration method for various types of linear and nonlinear partial differential equations. International Journal of Electrical and Computer Engineering, 13(2), 2131-2141.
Shirazian, M. (2023). A new acceleration of variational iteration method for initial value problems. Mathematics and Computer in Simulation, 204, 640-644.
Tebyakin, A. D., Kalutsky, L. A., Yakovleva, T. V., & Krysko, A. V. (2023). Application of Variational Iterations Method for Studying Physically and Geometrically Nonlinear Kirchhoff Nanoplates: A Mathematical Justification. Axioms, 12,
Tomar, S., Singh, M., Vajravedu, K., & Ramos, H. (2023). Simplifying the variational iteration method: A new approach to obtain the Lagrange multiplier. Mathematics and Computer in Simulation, 204, 640-644.
Yin, F., Song, J., & Cao, X. (2013). A General Iteration Formula of VIM for Fractional Heat- and Wave-Like Equations. Journal of Applied Mathematics, Article ID 428079.
Zabidi, N. U., Abdul-Majid, Z., Kilicman, A., & Rabiei, F. (2020). Numerical Solutions of Fractional Differential Equations by Using Fractional Explicit Adams Method, Mathematics, 8(1675), 1-23.
Zada, L., Nawaz, R., Ahsan, S., Nisar, K. S., & Baleanu, D. (2021). New iterative approach for the solutions of fractional order inhomogeneous partial differential equations, AIMS Mathematics, 6(2), 1348–1365.